The jSDM_binomial_logit function performs a Binomial logistic regression in a Bayesian framework. The function calls a Gibbs sampler written in 'C++' code which uses an adaptive Metropolis algorithm to estimate the conditional posterior distribution of model's parameters.
jSDM_binomial_logit(
burnin = 5000,
mcmc = 10000,
thin = 10,
presence_data,
site_formula,
trait_data = NULL,
trait_formula = NULL,
site_data,
trials = NULL,
n_latent = 0,
site_effect = "none",
beta_start = 0,
gamma_start = 0,
lambda_start = 0,
W_start = 0,
alpha_start = 0,
V_alpha = 1,
shape_Valpha = 0.5,
rate_Valpha = 5e-04,
mu_beta = 0,
V_beta = 10,
mu_gamma = 0,
V_gamma = 10,
mu_lambda = 0,
V_lambda = 10,
ropt = 0.44,
seed = 1234,
verbose = 1
)Arguments
- burnin
The number of burnin iterations for the sampler.
- mcmc
The number of Gibbs iterations for the sampler. Total number of Gibbs iterations is equal to
burnin+mcmc.burnin+mcmcmust be divisible by 10 and superior or equal to 100 so that the progress bar can be displayed.- thin
The thinning interval used in the simulation. The number of mcmc iterations must be divisible by this value.
- presence_data
A matrix \(n_{site} \times n_{species}\) indicating the number of successes (or presences) and the absence by a zero for each species at the studied sites.
- site_formula
A one-sided formula of the form '~x1+...+xp' specifying the explanatory variables for the suitability process of the model, used to form the design matrix \(X\) of size \(n_{site} \times np\).
- trait_data
A data frame containing the species traits which can be included as part of the model. Default to
NULLto fit a model without species traits.- trait_formula
A one-sided formula of the form '~ t1 + ... + tk + x1:t1 + ... + xp:tk' specifying the interactions between the environmental variables and the species traits to be considered in the model, used to form the trait design matrix \(Tr\) of size \(n_{species} \times nt\) and to set to \(0\) the \(\gamma\) parameters corresponding to interactions not taken into account according to the formula. Default to
NULLto fit a model with all possible interactions between species traits found intrait_dataand environmental variables defined bysite_formula.- site_data
A data frame containing the model's explanatory variables by site.
- trials
A vector indicating the number of trials for each site. \(n_i\) should be superior or equal to \(y_{ij}\), the number of successes for observation \(n\). If \(n_i=0\), then \(y_{ij}=0\). The default is one visit by site.
- n_latent
An integer which specifies the number of latent variables to generate. Defaults to \(0\).
- site_effect
A string indicating whether row effects are included as fixed effects (
"fixed"), as random effects ("random"), or not included ("none") in the model. If fixed effects, then for parameter identifiability the first row effect is set to zero, which analogous to acting as a reference level when dummy variables are used. If random effects, they are drawn from a normal distribution with mean zero and unknown variance, analogous to a random intercept in mixed models. Defaults to"none".- beta_start
Starting values for \(\beta\) parameters of the suitability process for each species must be either a scalar or a \(np \times n_{species}\) matrix. If
beta_starttakes a scalar value, then that value will serve for all of the \(\beta\) parameters.- gamma_start
Starting values for \(\gamma\) parameters that represent the influence of species-specific traits on species' responses \(\beta\),
gamma_startmust be either a scalar, a vector of length \(nt\), \(np\) or \(nt.np\) or a \(nt \times np\) matrix. Ifgamma_starttakes a scalar value, then that value will serve for all of the \(\gamma\) parameters. Ifgamma_startis a vector of length \(nt\) or \(nt.np\) the resulting \(nt \times np\) matrix is filled by column with specified values, if a \(np\)-length vector is given, the matrix is filled by row.- lambda_start
Starting values for \(\lambda\) parameters corresponding to the latent variables for each species must be either a scalar or a \(n_{latent} \times n_{species}\) upper triangular matrix with strictly positive values on the diagonal, ignored if
n_latent=0. Iflambda_starttakes a scalar value, then that value will serve for all of the \(\lambda\) parameters except those concerned by the constraints explained above.- W_start
Starting values for latent variables must be either a scalar or a \(nsite \times n_latent\) matrix, ignored if
n_latent=0. IfW_starttakes a scalar value, then that value will serve for all of the \(W_{il}\) with \(i=1,\ldots,n_{site}\) and \(l=1,\ldots,n_{latent}\).- alpha_start
Starting values for random site effect parameters must be either a scalar or a \(n_{site}\)-length vector, ignored if
site_effect="none". Ifalpha_starttakes a scalar value, then that value will serve for all of the \(\alpha\) parameters.- V_alpha
Starting value for variance of random site effect if
site_effect="random"or constant variance of the Gaussian prior distribution for the fixed site effect ifsite_effect="fixed". Must be a strictly positive scalar, ignored ifsite_effect="none".- shape_Valpha
Shape parameter of the Inverse-Gamma prior for the random site effect variance
V_alpha, ignored ifsite_effect="none"orsite_effect="fixed". Must be a strictly positive scalar. Default to 0.5 for weak informative prior.- rate_Valpha
Rate parameter of the Inverse-Gamma prior for the random site effect variance
V_alpha, ignored ifsite_effect="none"orsite_effect="fixed"Must be a strictly positive scalar. Default to 0.0005 for weak informative prior.- mu_beta
Means of the Normal priors for the \(\beta\) parameters of the suitability process.
mu_betamust be either a scalar or a \(np\)-length vector. Ifmu_betatakes a scalar value, then that value will serve as the prior mean for all of the \(\beta\) parameters. The default value is set to 0 for an uninformative prior, ignored iftrait_datais specified.- V_beta
Variances of the Normal priors for the \(\beta\) parameters of the suitability process.
V_betamust be either a scalar or a \(np \times np\) symmetric positive semi-definite square matrix. IfV_betatakes a scalar value, then that value will serve as the prior variance for all of the \(\beta\) parameters, so the variance covariance matrix used in this case is diagonal with the specified value on the diagonal. The default variance is large and set to 10 for an uninformative flat prior.- mu_gamma
Means of the Normal priors for the \(\gamma\) parameters.
mu_gammamust be either a scalar, a vector of length \(nt\), \(np\) or \(nt.np\) or a \(nt \times np\) matrix. Ifmu_gammatakes a scalar value, then that value will serve as the prior mean for all of the \(\gamma\) parameters. Ifmu_gammais a vector of length \(nt\) or \(nt.np\) the resulting \(nt \times np\) matrix is filled by column with specified values, if a \(np\)-length vector is given, the matrix is filled by row. The default value is set to 0 for an uninformative prior, ignored iftrait_data=NULL.- V_gamma
Variances of the Normal priors for the \(\gamma\) parameters.
V_gammamust be either a scalar, a vector of length \(nt\), \(np\) or \(nt.np\) or a \(nt \times np\) positive matrix. IfV_gammatakes a scalar value, then that value will serve as the prior variance for all of the \(\gamma\) parameters. IfV_gammais a vector of length \(nt\) or \(nt.np\) the resulting \(nt \times np\) matrix is filled by column with specified values, if a \(np\)-length vector is given, the matrix is filled by row. The default variance is large and set to 10 for an uninformative flat prior, ignored iftrait_data=NULL.- mu_lambda
Means of the Normal priors for the \(\lambda\) parameters corresponding to the latent variables.
mu_lambdamust be either a scalar or a \(n_{latent}\)-length vector. Ifmu_lambdatakes a scalar value, then that value will serve as the prior mean for all of the \(\lambda\) parameters. The default value is set to 0 for an uninformative prior.- V_lambda
Variances of the Normal priors for the \(\lambda\) parameters corresponding to the latent variables.
V_lambdamust be either a scalar or a \(n_{latent} \times n_{latent}\) symmetric positive semi-definite square matrix. IfV_lambdatakes a scalar value, then that value will serve as the prior variance for all of \(\lambda\) parameters, so the variance covariance matrix used in this case is diagonal with the specified value on the diagonal. The default variance is large and set to 10 for an uninformative flat prior.- ropt
Target acceptance rate for the adaptive Metropolis algorithm. Default to 0.44.
- seed
The seed for the random number generator. Default to 1234.
- verbose
A switch (0,1) which determines whether or not the progress of the sampler is printed to the screen. Default is 1: a progress bar is printed, indicating the step (in %) reached by the Gibbs sampler.
Value
An object of class "jSDM" acting like a list including :
- mcmc.alpha
An mcmc object that contains the posterior samples for site effects \(\alpha_i\), not returned if
site_effect="none".- mcmc.V_alpha
An mcmc object that contains the posterior samples for variance of random site effect, not returned if
site_effect="none"orsite_effect="fixed".- mcmc.latent
A list by latent variable of mcmc objects that contains the posterior samples for latent variables \(W_l\) with \(l=1,\ldots,n_{latent}\), not returned if
n_latent=0.- mcmc.sp
A list by species of mcmc objects that contains the posterior samples for species effects \(\beta_j\) and \(\lambda_j\) if
n_latent>0.- mcmc.gamma
A list by covariates of mcmc objects that contains the posterior samples for \(\gamma_p\) parameters with \(p=1,\ldots,np\) if
trait_datais specified.- mcmc.Deviance
The posterior sample of the deviance (\(D\)) is also provided, with \(D\) defined as : \(D=-2\log(\prod_{ij} P(y_{ij}|\beta_j,\lambda_j, \alpha_i, W_i))\).
- logit_theta_latent
Predictive posterior mean of the probability to each species to be present on each site, transformed by logit link function.
- theta_latent
Predictive posterior mean of the probability associated to the suitability process for each observation.
- model_spec
Various attributes of the model fitted, including the response and model matrix used, distributional assumptions as link function, family and number of latent variables, hyperparameters used in the Bayesian estimation and mcmc, burnin and thin.
The mcmc. objects can be summarized by functions provided by the coda package.
Details
We model an ecological process where the presence or absence of species \(j\) on site \(i\) is explained by habitat suitability.
Ecological process : $$y_{ij} \sim \mathcal{B}inomial(\theta_{ij},n_i)$$ where
if n_latent=0 and site_effect="none" | logit\((\theta_{ij}) = X_i \beta_j\) |
if n_latent>0 and site_effect="none" | logit\((\theta_{ij}) = X_i \beta_j + W_i \lambda_j\) |
if n_latent=0 and site_effect="fixed" | logit\((\theta_{ij}) = X_i \beta_j + \alpha_i\) |
if n_latent>0 and site_effect="fixed" | logit\((\theta_{ij}) = X_i \beta_j + W_i \lambda_j + \alpha_i\) |
if n_latent=0 and site_effect="random" | logit\((\theta_{ij}) = X_i \beta_j + \alpha_i\) and \(\alpha_i \sim \mathcal{N}(0,V_\alpha)\) |
if n_latent>0 and site_effect="random" | logit\((\theta_{ij}) = X_i \beta_j + W_i \lambda_j + \alpha_i\) and \(\alpha_i \sim \mathcal{N}(0,V_\alpha)\) |
In the absence of data on species traits (trait_data=NULL), the effect of species \(j\): \(\beta_j\);
follows the same a priori Gaussian distribution such that \(\beta_j \sim \mathcal{N}_{np}(\mu_{\beta},V_{\beta})\),
for each species.
If species traits data are provided, the effect of species \(j\): \(\beta_j\); follows an a priori Gaussian distribution such that \(\beta_j \sim \mathcal{N}_{np}(\mu_{\beta_j},V_{\beta})\), where \(\mu_{\beta_jp} = \sum_{k=1}^{nt} t_{jk}.\gamma_{kp}\), takes different values for each species.
We assume that \(\gamma_{kp} \sim \mathcal{N}(\mu_{\gamma_{kp}},V_{\gamma_{kp}})\) as prior distribution.
We define the matrix \(\gamma=(\gamma_{kp})_{k=1,...,nt}^{p=1,...,np}\) such as :
| \(x_0\) | \(x_1\) | ... | \(x_p\) | ... | \(x_{np}\) | ||
| __________ | ________ | ________ | ________ | ________ | ________ | ||
| \(t_0\) | | \(\gamma_{0,0}\) | \(\gamma_{0,1}\) | ... | \(\gamma_{0,p}\) | ... | \(\gamma_{0,np}\) | { effect of |
| | | intercept | environmental | |||||
| | | variables | ||||||
| \(t_1\) | | \(\gamma_{1,0}\) | \(\gamma_{1,1}\) | ... | \(\gamma_{1,p}\) | ... | \(\gamma_{1,np}\) | |
| ... | | ... | ... | ... | ... | ... | ... | |
| \(t_k\) | | \(\gamma_{k,0}\) | \(\gamma_{k,1}\) | ... | \(\gamma_{k,p}\) | ... | \(\gamma_{k,np}\) | |
| ... | | ... | ... | ... | ... | ... | ... | |
| \(t_{nt}\) | | \(\gamma_{nt,0}\) | \(\gamma_{nt,1}\) | ... | \(\gamma_{nt,p}\) | ... | \(\gamma_{nt,np}\) | |
| average | |||||||
| trait effect | interaction | traits | environment |
References
Gelfand, A. E.; Schmidt, A. M.; Wu, S.; Silander, J. A.; Latimer, A. and Rebelo, A. G. (2005) Modelling species diversity through species level hierarchical modelling. Applied Statistics, 54, 1-20.
Latimer, A. M.; Wu, S. S.; Gelfand, A. E. and Silander, J. A. (2006) Building statistical models to analyze species distributions. Ecological Applications, 16, 33-50.
Ovaskainen, O., Tikhonov, G., Norberg, A., Blanchet, F. G., Duan, L., Dunson, D., Roslin, T. and Abrego, N. (2017) How to make more out of community data? A conceptual framework and its implementation as models and software. Ecology Letters, 20, 561-576.
Examples
#==============================================
# jSDM_binomial_logit()
# Example with simulated data
#==============================================
#=================
#== Load libraries
library(jSDM)
#==================
#== Data simulation
#= Number of sites
nsite <- 50
#= Number of species
nsp <- 10
#= Set seed for repeatability
seed <- 1234
#= Number of visits associated to each site
set.seed(seed)
visits <- rpois(nsite,3)
visits[visits==0] <- 1
#= Ecological process (suitability)
x1 <- rnorm(nsite,0,1)
set.seed(2*seed)
x2 <- rnorm(nsite,0,1)
X <- cbind(rep(1,nsite),x1,x2)
np <- ncol(X)
set.seed(3*seed)
W <- cbind(rnorm(nsite,0,1),rnorm(nsite,0,1))
n_latent <- ncol(W)
l.zero <- 0
l.diag <- runif(2,0,2)
l.other <- runif(nsp*2-3,-2,2)
lambda.target <- matrix(c(l.diag[1],l.zero,l.other[1],
l.diag[2],l.other[-1]),
byrow=TRUE, nrow=nsp)
beta.target <- matrix(runif(nsp*np,-2,2), byrow=TRUE, nrow=nsp)
V_alpha.target <- 0.5
alpha.target <- rnorm(nsite,0,sqrt(V_alpha.target))
logit.theta <- X %*% t(beta.target) + W %*% t(lambda.target) + alpha.target
theta <- inv_logit(logit.theta)
set.seed(seed)
Y <- apply(theta, 2, rbinom, n=nsite, size=visits)
#= Site-occupancy model
# Increase number of iterations (burnin and mcmc) to get convergence
mod <- jSDM_binomial_logit(# Chains
burnin=150,
mcmc=150,
thin=1,
# Response variable
presence_data=Y,
trials=visits,
# Explanatory variables
site_formula=~x1+x2,
site_data=X,
n_latent=n_latent,
site_effect="random",
# Starting values
beta_start=0,
lambda_start=0,
W_start=0,
alpha_start=0,
V_alpha=1,
# Priors
shape_Valpha=0.5,
rate_Valpha=0.0005,
mu_beta=0,
V_beta=10,
mu_lambda=0,
V_lambda=10,
# Various
seed=1234,
ropt=0.44,
verbose=1)
#>
#> Running the Gibbs sampler. It may be long, please keep cool :)
#>
#> **********:10.0%, mean accept. rates= beta:0.287 lambda:0.349 W:0.508 alpha:0.368
#> **********:20.0%, mean accept. rates= beta:0.342 lambda:0.372 W:0.432 alpha:0.369
#> **********:30.0%, mean accept. rates= beta:0.429 lambda:0.372 W:0.438 alpha:0.230
#> **********:40.0%, mean accept. rates= beta:0.436 lambda:0.447 W:0.419 alpha:0.242
#> **********:50.0%, mean accept. rates= beta:0.454 lambda:0.453 W:0.439 alpha:0.376
#> **********:60.0%, mean accept. rates= beta:0.437 lambda:0.433 W:0.435 alpha:0.592
#> **********:70.0%, mean accept. rates= beta:0.434 lambda:0.489 W:0.443 alpha:0.689
#> **********:80.0%, mean accept. rates= beta:0.451 lambda:0.451 W:0.446 alpha:0.715
#> **********:90.0%, mean accept. rates= beta:0.444 lambda:0.449 W:0.429 alpha:0.722
#> **********:100.0%, mean accept. rates= beta:0.418 lambda:0.454 W:0.442 alpha:0.677
#==========
#== Outputs
#= Parameter estimates
oldpar <- par(no.readonly = TRUE)
## beta_j
# summary(mod$mcmc.sp$sp_1[,1:ncol(X)])
mean_beta <- matrix(0,nsp,np)
pdf(file=file.path(tempdir(), "Posteriors_beta_jSDM_logit.pdf"))
par(mfrow=c(ncol(X),2))
for (j in 1:nsp) {
mean_beta[j,] <- apply(mod$mcmc.sp[[j]][,1:ncol(X)],
2, mean)
for (p in 1:ncol(X)) {
coda::traceplot(mod$mcmc.sp[[j]][,p])
coda::densplot(mod$mcmc.sp[[j]][,p],
main = paste(colnames(
mod$mcmc.sp[[j]])[p],
", species : ",j))
abline(v=beta.target[j,p],col='red')
}
}
dev.off()
#> agg_record_1733169229
#> 2
## lambda_j
mean_lambda <- matrix(0,nsp,n_latent)
pdf(file=file.path(tempdir(), "Posteriors_lambda_jSDM_logit.pdf"))
par(mfrow=c(n_latent*2,2))
for (j in 1:nsp) {
mean_lambda[j,] <- apply(mod$mcmc.sp[[j]]
[,(ncol(X)+1):(ncol(X)+n_latent)], 2, mean)
for (l in 1:n_latent) {
coda::traceplot(mod$mcmc.sp[[j]][,ncol(X)+l])
coda::densplot(mod$mcmc.sp[[j]][,ncol(X)+l],
main=paste(colnames(mod$mcmc.sp[[j]])
[ncol(X)+l],", species : ",j))
abline(v=lambda.target[j,l],col='red')
}
}
dev.off()
#> agg_record_1733169229
#> 2
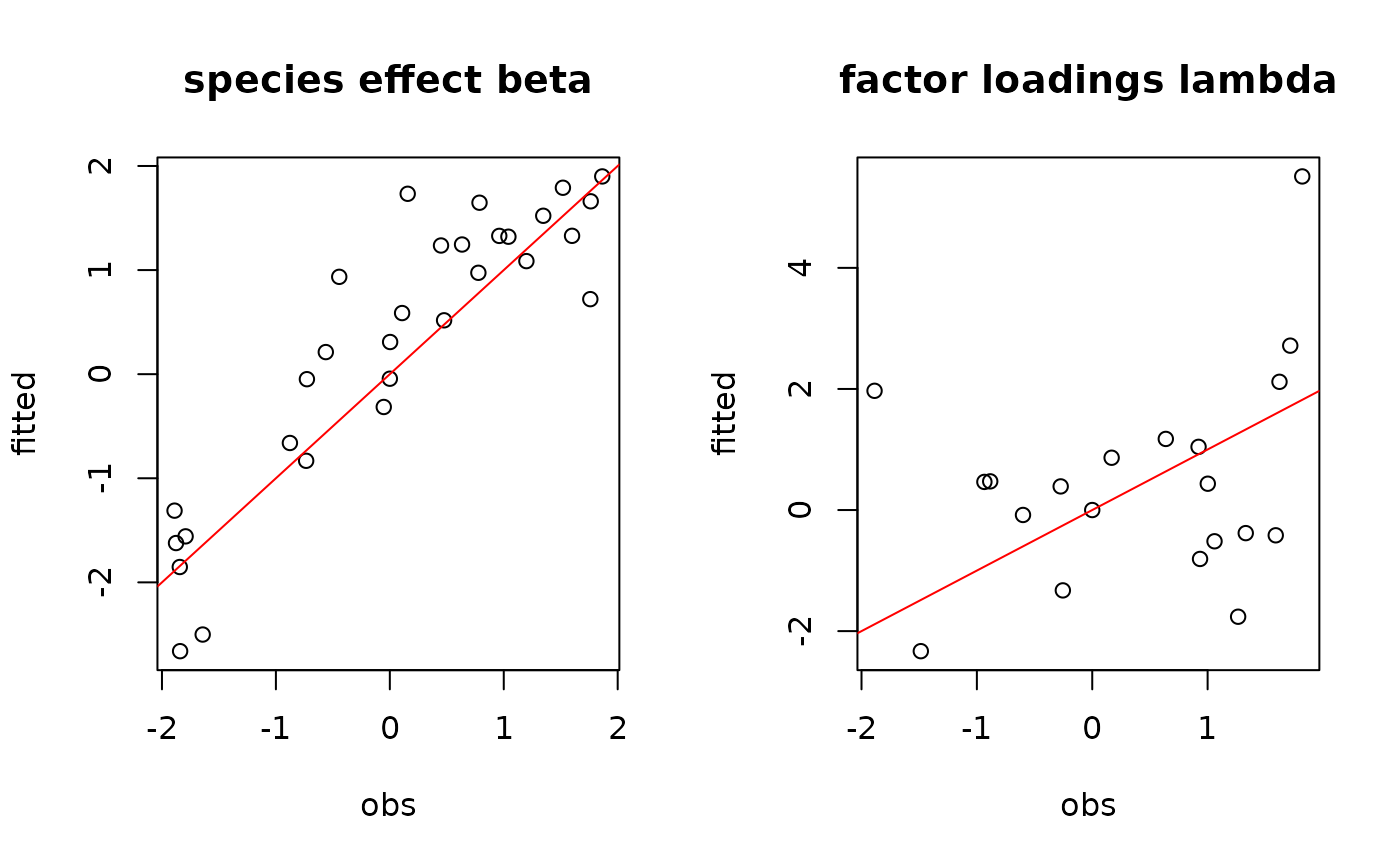
# Species effects beta and factor loadings lambda
par(mfrow=c(1,2))
plot(beta.target, mean_beta,
main="species effect beta",
xlab ="obs", ylab ="fitted")
abline(a=0,b=1,col='red')
plot(lambda.target, mean_lambda,
main="factor loadings lambda",
xlab ="obs", ylab ="fitted")
abline(a=0,b=1,col='red')
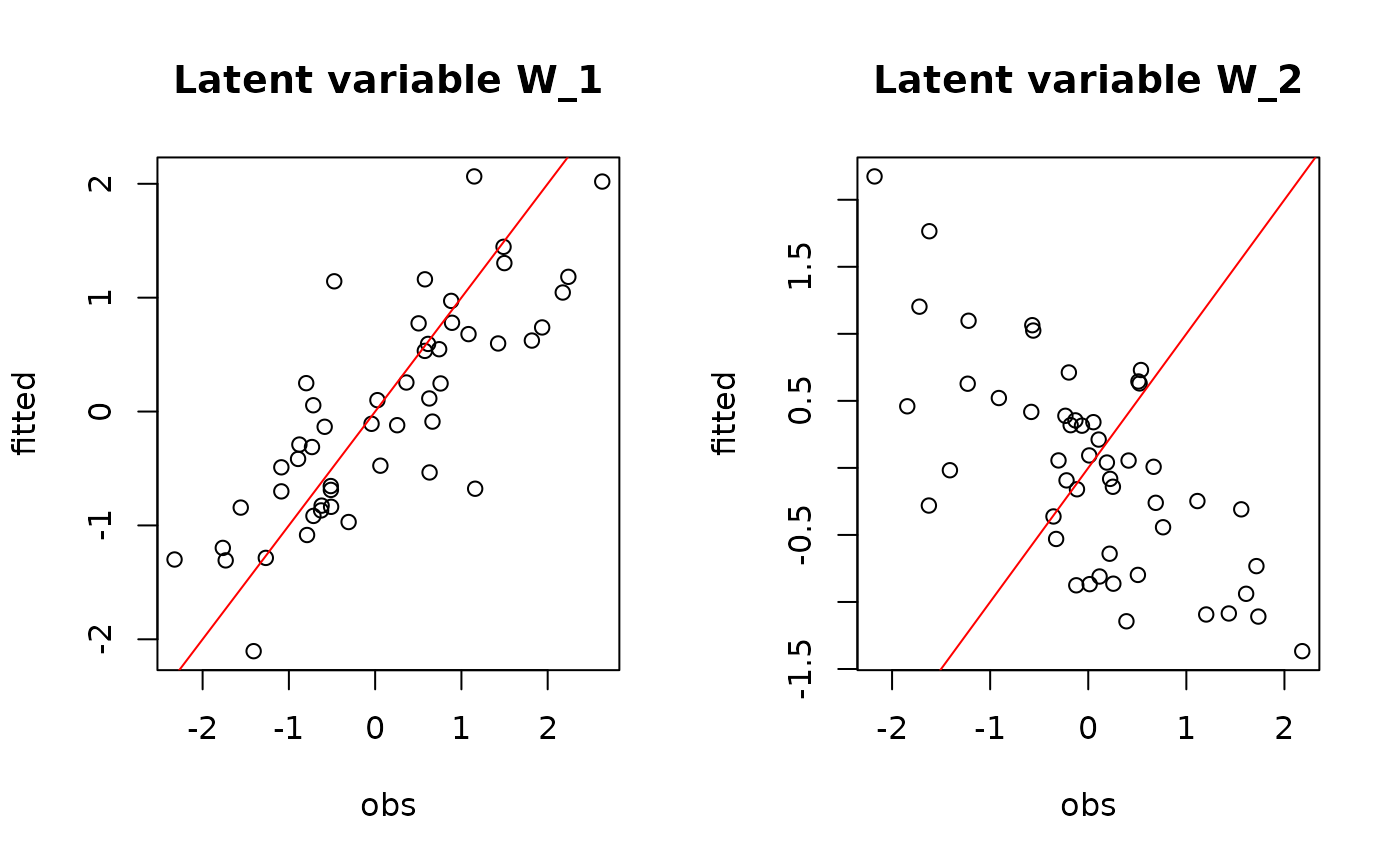
 ## W latent variables
par(mfrow=c(1,2))
for (l in 1:n_latent) {
plot(W[,l],
summary(mod$mcmc.latent[[paste0("lv_",l)]])[[1]][,"Mean"],
main = paste0("Latent variable W_", l),
xlab ="obs", ylab ="fitted")
abline(a=0,b=1,col='red')
}
## W latent variables
par(mfrow=c(1,2))
for (l in 1:n_latent) {
plot(W[,l],
summary(mod$mcmc.latent[[paste0("lv_",l)]])[[1]][,"Mean"],
main = paste0("Latent variable W_", l),
xlab ="obs", ylab ="fitted")
abline(a=0,b=1,col='red')
}
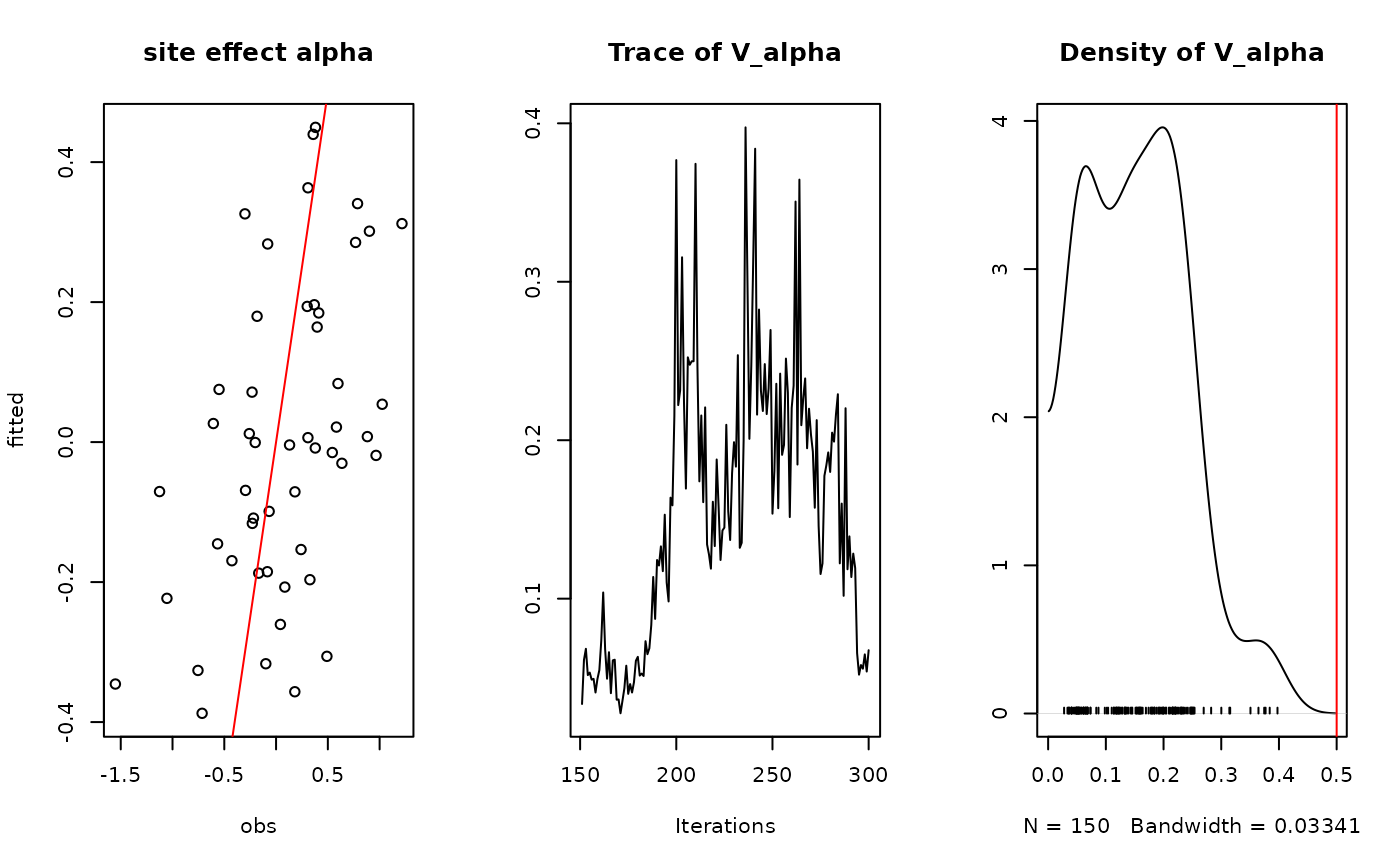
 ## alpha
par(mfrow=c(1,3))
plot(alpha.target, summary(mod$mcmc.alpha)[[1]][,"Mean"],
xlab ="obs", ylab ="fitted", main="site effect alpha")
abline(a=0,b=1,col='red')
## Valpha
coda::traceplot(mod$mcmc.V_alpha)
coda::densplot(mod$mcmc.V_alpha)
abline(v=V_alpha.target,col='red')
## alpha
par(mfrow=c(1,3))
plot(alpha.target, summary(mod$mcmc.alpha)[[1]][,"Mean"],
xlab ="obs", ylab ="fitted", main="site effect alpha")
abline(a=0,b=1,col='red')
## Valpha
coda::traceplot(mod$mcmc.V_alpha)
coda::densplot(mod$mcmc.V_alpha)
abline(v=V_alpha.target,col='red')
 ## Deviance
summary(mod$mcmc.Deviance)
#>
#> Iterations = 151:300
#> Thinning interval = 1
#> Number of chains = 1
#> Sample size per chain = 150
#>
#> 1. Empirical mean and standard deviation for each variable,
#> plus standard error of the mean:
#>
#> Mean SD Naive SE Time-series SE
#> 699.266 21.720 1.773 5.062
#>
#> 2. Quantiles for each variable:
#>
#> 2.5% 25% 50% 75% 97.5%
#> 659.4 686.5 697.7 712.2 743.8
#>
plot(mod$mcmc.Deviance)
## Deviance
summary(mod$mcmc.Deviance)
#>
#> Iterations = 151:300
#> Thinning interval = 1
#> Number of chains = 1
#> Sample size per chain = 150
#>
#> 1. Empirical mean and standard deviation for each variable,
#> plus standard error of the mean:
#>
#> Mean SD Naive SE Time-series SE
#> 699.266 21.720 1.773 5.062
#>
#> 2. Quantiles for each variable:
#>
#> 2.5% 25% 50% 75% 97.5%
#> 659.4 686.5 697.7 712.2 743.8
#>
plot(mod$mcmc.Deviance)
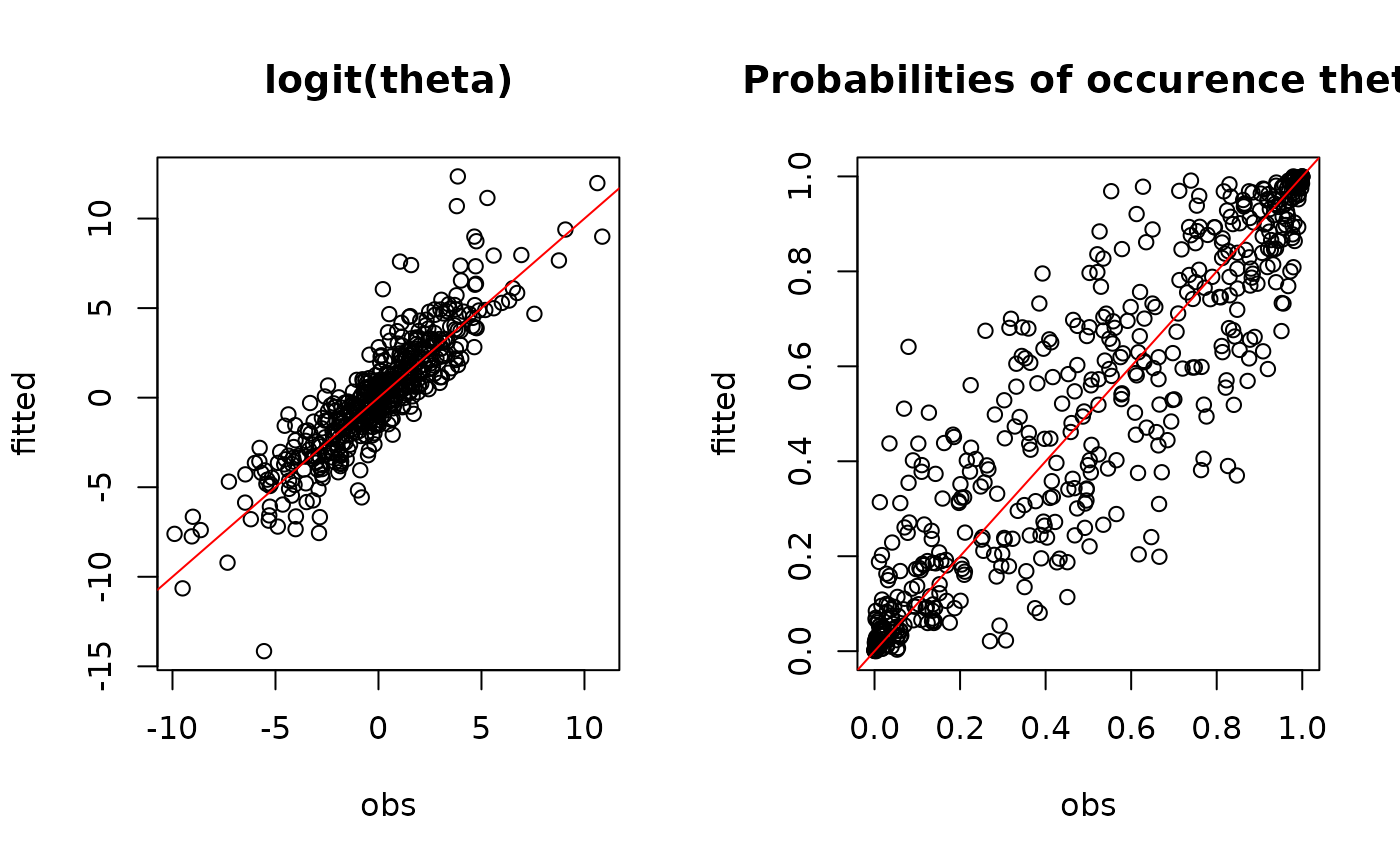
 #= Predictions
par(mfrow=c(1,2))
plot(logit.theta, mod$logit_theta_latent,
main="logit(theta)",
xlab="obs", ylab="fitted")
abline(a=0 ,b=1, col="red")
plot(theta, mod$theta_latent,
main="Probabilities of occurence theta",
xlab="obs", ylab="fitted")
abline(a=0 ,b=1, col="red")
#= Predictions
par(mfrow=c(1,2))
plot(logit.theta, mod$logit_theta_latent,
main="logit(theta)",
xlab="obs", ylab="fitted")
abline(a=0 ,b=1, col="red")
plot(theta, mod$theta_latent,
main="Probabilities of occurence theta",
xlab="obs", ylab="fitted")
abline(a=0 ,b=1, col="red")
 par(oldpar)
par(oldpar)