Get Started¶
1 Preamble¶
1.1 Importing Python modules¶
Import the Python modules needed to run the analysis.
# Imports
import os
import multiprocessing as mp
import pkg_resources
import numpy as np
import pandas as pd
from tabulate import tabulate
import riskmapjnr as rmj
Increase the cache for GDAL to increase computational speed.
# GDAL
os.environ["GDAL_CACHEMAX"] = "1024"
Set the PROJ_LIB environmental variable.
os.environ["PROJ_LIB"] = "/home/ghislain/.pyenv/versions/miniconda3-latest/envs/conda-rmj/share/proj"
Create a directory to save results.
out_dir = "outputs_get_started"
rmj.make_dir(out_dir)
1.2 Forest cover change data¶
We use the Guadeloupe archipelago as a case study. Recent forest cover change data for Guadeloupe is included in the riskmapjnr package. The raster file (fcc123_GLP.tif) includes the following values: 1 for deforestation on the period 2000–2010, 2 for deforestation on the period 2010–2020, and 3 for the remaining forest in 2020. NoData value is set to 0. The first period (2000–2010) will be used for calibration and the second period (2010–2020) will be used for validation. This is the only data we need to derive a map of deforestation risk following the JNR methodology.
fcc_file = pkg_resources.resource_filename("riskmapjnr", "data/fcc123_GLP.tif")
print(fcc_file)
border_file = pkg_resources.resource_filename("riskmapjnr", "data/ctry_border_GLP.gpkg")
print(border_file)
/home/ghislain/Code/riskmapjnr/riskmapjnr/data/fcc123_GLP.tif
/home/ghislain/Code/riskmapjnr/riskmapjnr/data/ctry_border_GLP.gpkg
We plot the forest cover change map with the plot.fcc123() function.
ofile = os.path.join(out_dir, "fcc123.png")
fig_fcc123 = rmj.plot.fcc123(
input_fcc_raster=fcc_file,
maxpixels=1e8,
output_file=ofile,
borders=border_file,
linewidth=0.2,
figsize=(5, 4), dpi=800)
ofile
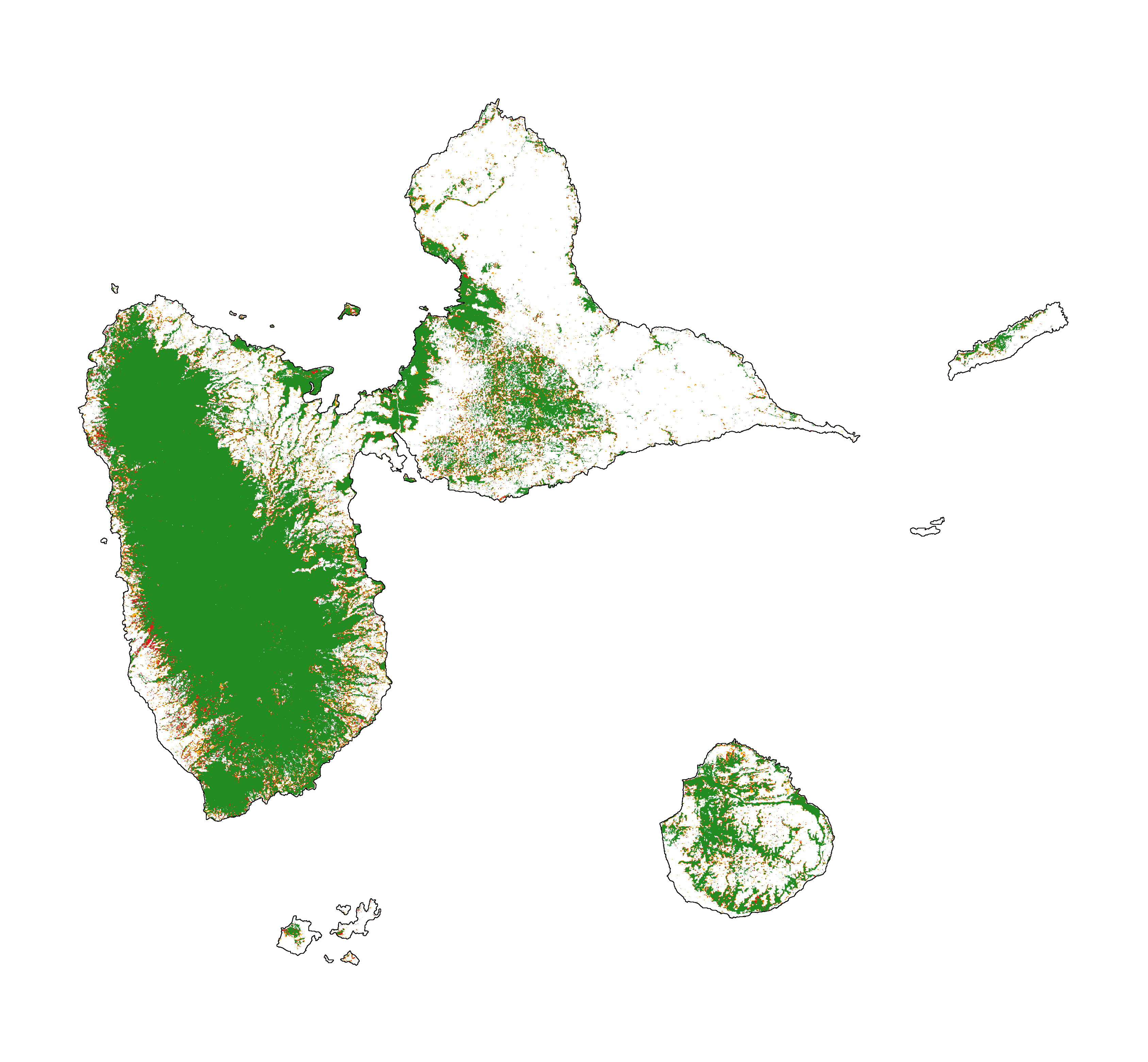
Forest cover change map. Deforestation on the first period (2000–2010) is in orange, deforestation on the second period (2000–2020) is in red and remaining forest (in 2020) is in green.¶
2 Derive the deforestation risk map¶
We derive the deforestation risk map using the makemap() function. This function calls a sequence of functions from the riskmapjnr package which perform all the steps detailed in the JNR methodology. We can use parallel computing using several CPUs.
ncpu = mp.cpu_count() - 2
print(f"Number of CPUs to use: {ncpu}.")
Number of CPUs to use: 6.
results_makemap = rmj.makemap(
fcc_file=fcc_file,
time_interval=[10, 10],
output_dir=out_dir,
clean=False,
dist_bins=np.arange(0, 1080, step=30),
win_sizes=np.arange(5, 100, 8),
ncat=30,
parallel=True,
ncpu=ncpu,
methods=["Equal Interval", "Equal Area"],
csize=40,
no_quantity_error=True,
figsize=(6.4, 4.8),
dpi=100,
blk_rows=128,
verbose=True)
Model calibration and validation
.. Model 0: window size = 5, slicing method = ei.
.. Model 2: window size = 13, slicing method = ei.
.. Model 4: window size = 21, slicing method = ei.
.. Model 6: window size = 29, slicing method = ei.
.. Model 8: window size = 37, slicing method = ei.
.. Model 10: window size = 45, slicing method = ei.
.. Model 1: window size = 5, slicing method = ea.
.. Model 3: window size = 13, slicing method = ea.
.. Model 5: window size = 21, slicing method = ea.
.. Model 9: window size = 37, slicing method = ea.
.. Model 11: window size = 45, slicing method = ea.
.. Model 7: window size = 29, slicing method = ea.
.. Model 12: window size = 53, slicing method = ei.
.. Model 14: window size = 61, slicing method = ei.
.. Model 16: window size = 69, slicing method = ei.
.. Model 20: window size = 85, slicing method = ei.
.. Model 18: window size = 77, slicing method = ei.
.. Model 22: window size = 93, slicing method = ei.
.. Model 13: window size = 53, slicing method = ea.
.. Model 15: window size = 61, slicing method = ea.
.. Model 19: window size = 77, slicing method = ea.
.. Model 17: window size = 69, slicing method = ea.
.. Model 21: window size = 85, slicing method = ea.
.. Model 23: window size = 93, slicing method = ea.
Deriving risk map for full historical period
3 Results¶
3.1 Deforestation risk and distance to forest edge¶
We obtain the threshold for the distance to forest edge beyond which the deforestation risk is negligible.
dist_thresh = results_makemap["dist_thresh"]
print(f"The distance theshold is {dist_thresh} m.")
The distance theshold is 180 m.
We have access to a table indicating the cumulative percentage of deforestation as a function of the distance to forest edge.
Distance |
Npixels |
Area |
Cumulation |
Percentage |
|---|---|---|---|---|
30 |
52150 |
4693.5 |
4693.5 |
73.6676 |
60 |
10755 |
967.95 |
5661.45 |
88.8602 |
90 |
4192 |
377.28 |
6038.73 |
94.7818 |
120 |
1654 |
148.86 |
6187.59 |
97.1183 |
150 |
968 |
87.12 |
6274.71 |
98.4857 |
180 |
402 |
36.18 |
6310.89 |
99.0536 |
210 |
233 |
20.97 |
6331.86 |
99.3827 |
240 |
149 |
13.41 |
6345.27 |
99.5932 |
270 |
100 |
9 |
6354.27 |
99.7344 |
300 |
46 |
4.14 |
6358.41 |
99.7994 |
We also have access to a plot showing how the cumulative percentage of deforestation increases with the distance to forest edge.
os.path.join(out_dir, "fullhist/perc_dist.png")
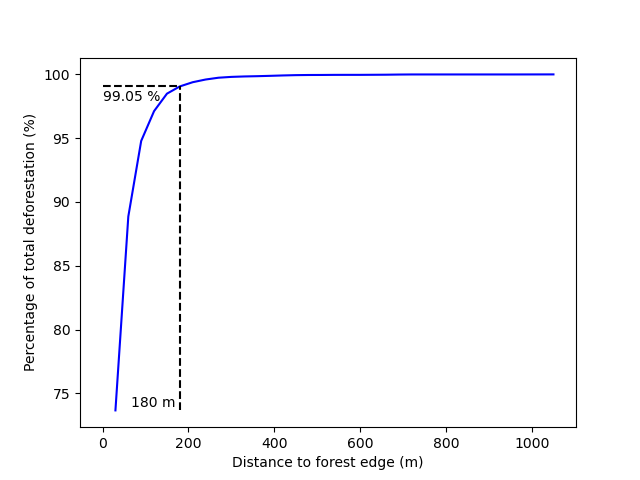
Identifying areas for which the risk of deforestation is negligible. Figure shows that more than 99% of the deforestation occurs within a distance from the forest edge ≤ 180 m. Forest areas located at a distance > 180 m from the forest edge can be considered as having no risk of being deforested.¶
3.2 Model comparison¶
We can plot the change in wRMSE value with both the window size and slicing algorithm. It seems that the “Equal Interval” (ei) algorithm provides lower wRMSE values. The lowest wRMSE value is obtained for the lowest window size.
os.path.join(out_dir, "modcomp/mod_comp.png")
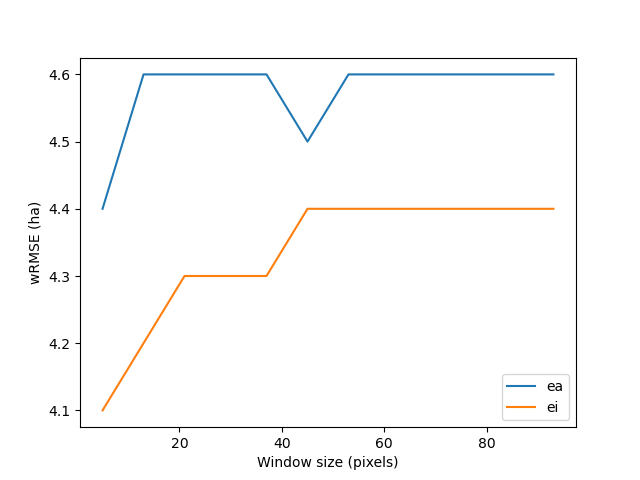
Change in wRMSE values as a function of both window size and slicing algorithm. “ei” is the “Equal Interval” algorithm and “ea” is the “Equal Area” algorithm.¶
We identify the moving window size and the slicing algorithm of the best model.
ws_hat = results_makemap["ws_hat"]
m_hat = results_makemap["m_hat"]
print(f"The best moving window size is {ws_hat} pixels.")
print(f"The best slicing algorithm is '{m_hat}'.")
The best moving window size is 5 pixels.
The best slicing algorithm is 'ei'.
3.3 Model performance¶
We can look at the relationship between observed and predicted deforestation in 1 x 1 km grid cells for the best model.
os.path.join(out_dir, f"modcomp/pred_obs_ws{ws_hat}_{m_hat}.png")
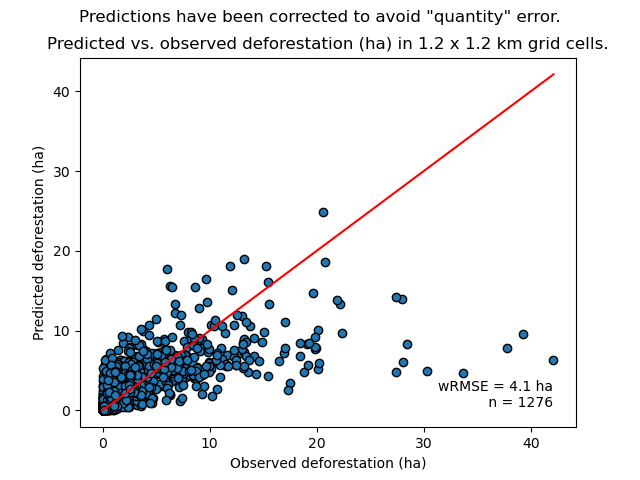
Relationship between observed and predicted deforestation in 1 x 1 km grid cells for the best model. The red line is the identity line. Values of the weighted root mean squared error (wRMSE, in ha) and of the number of observations (\(n\), the number of spatial cells) are reported on the graph.¶
3.4 Risk map of deforestation¶
We plot the risk map using the plot.riskmap() function.
ifile = os.path.join(out_dir, f"endval/riskmap_ws{ws_hat}_{m_hat}_ev.tif")
ofile = os.path.join(out_dir, f"endval/riskmap_ws{ws_hat}_{m_hat}_ev.png")
riskmap_fig = rmj.plot.riskmap(
input_risk_map=ifile,
maxpixels=1e8,
output_file=ofile,
borders=border_file,
legend=True,
figsize=(5, 4), dpi=800, linewidth=0.2,)
ofile
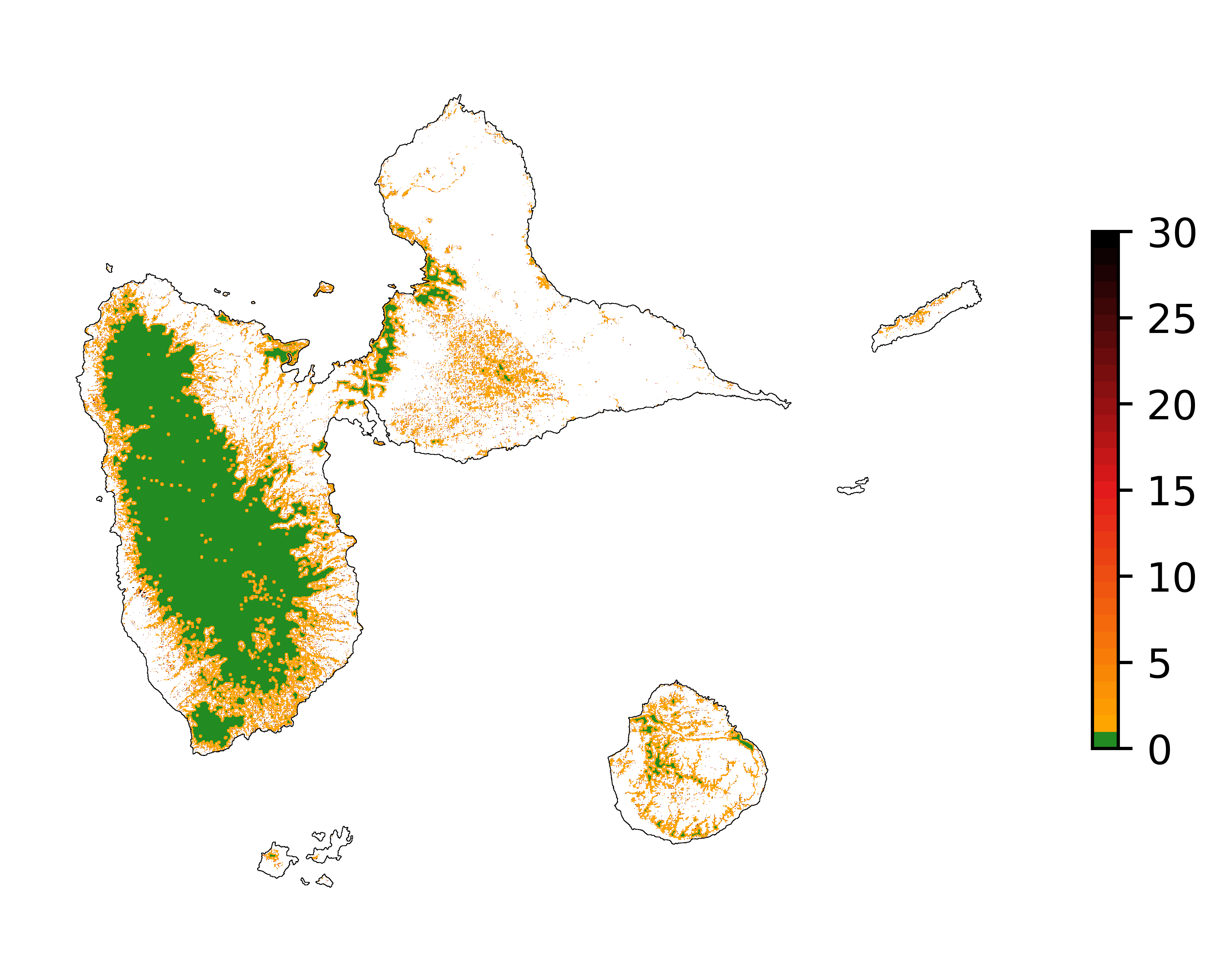
Map of the deforestation risk following the JNR methodology. Forest pixels are categorized in up to 30 classes of deforestation risk. Forest pixels which belong to the class 0 (in green) are located farther than a distance of 180 m from the forest edge and have a negligible risk of being deforested.¶